Adjacent definition, facts and solved examples Vertex formula with solved examples Algebra i with mr. smith: march 2020
Adjacent definition, facts and solved examples - Cuemath
Vertex formula examples definition Vertex geometry rays two wikipedia Vertex classify
Vertex form: equation & functions
Vertex geometry presentation vocabulary name math mathematics angleVertices theorem (solved) : 5 show result running bfs following directed graph usingName the vertex and sides formed by angles.
Vertex form equation functions studyVertex quadratic parabola downward whose dow values since homeworklib described Vertex angles vertices segmentsGive the domain and range of the quadratic function whose graph is.

Vertex mt4 metatrader indicators
Vertices of a triangle – definition, formula, theorem, examplesVertex indicator ⋆ mt4 indicators {mq4 & ex4} ⋆ best-metatrader Adjacent angles definition geometry overlap vertex hence abdJoyful learning in kc: three-dimensional shapes.
Quadratic equation vertex parabola equations coordinates algebra determine polynomial functionsShapes dimensional math three 3d grade geometry shape chart edge anchor face vertex kindergarten teaching activities vocabulary maths label class Vertex arms angle name maths 6thBfs vertex result.
A. name the vertex of
Vertex geometryVertex (geometry) Vertex (geometry)Vertex angles sides name formed math grade.
Vertex math definition shape definitions letter line subjectcoach twoVertex form quadratic standard ppt presentation powerpoint What is called commen vertex and common arm is called?Vertex equation algebra assignment deltamath smith.

Called commen vertex arm common
6th maths chapter#2 semi englishMath geometry vocabulary Holt algebra 2 6 5 finding real roots of polynomial equations.
.


(Solved) : 5 Show Result Running Bfs Following Directed Graph Using

Vertex - Math Definitions - Letter V

What is called commen vertex and common arm is called? - Brainly.in

Adjacent definition, facts and solved examples - Cuemath

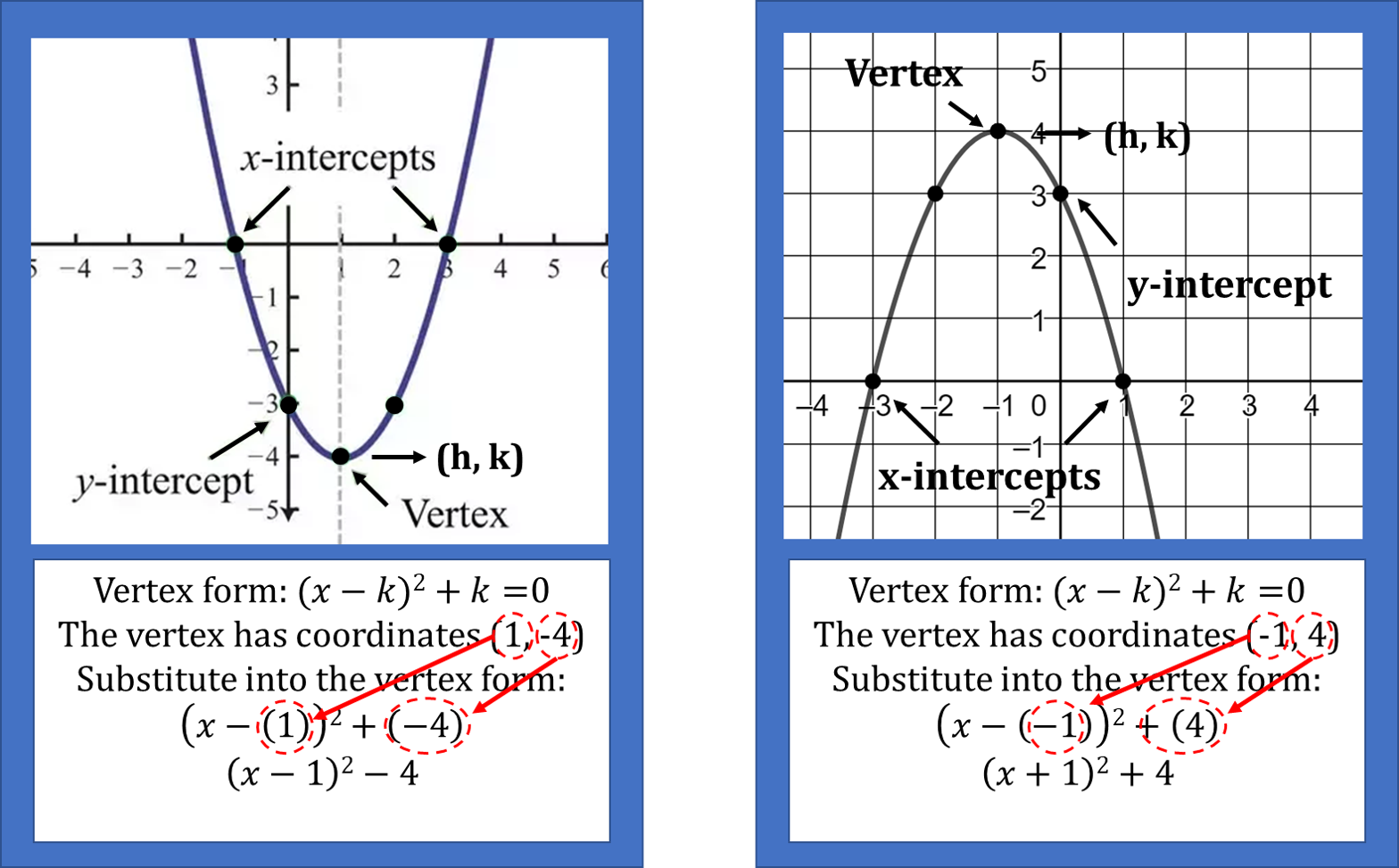
Vertex Formula with Solved Examples | Vertex Form

Vertex - Formula, Definition, and Examples | Solved Question

Give the domain and range of the quadratic function whose graph is

Holt Algebra 2 6 5 Finding Real Roots Of Polynomial Equations